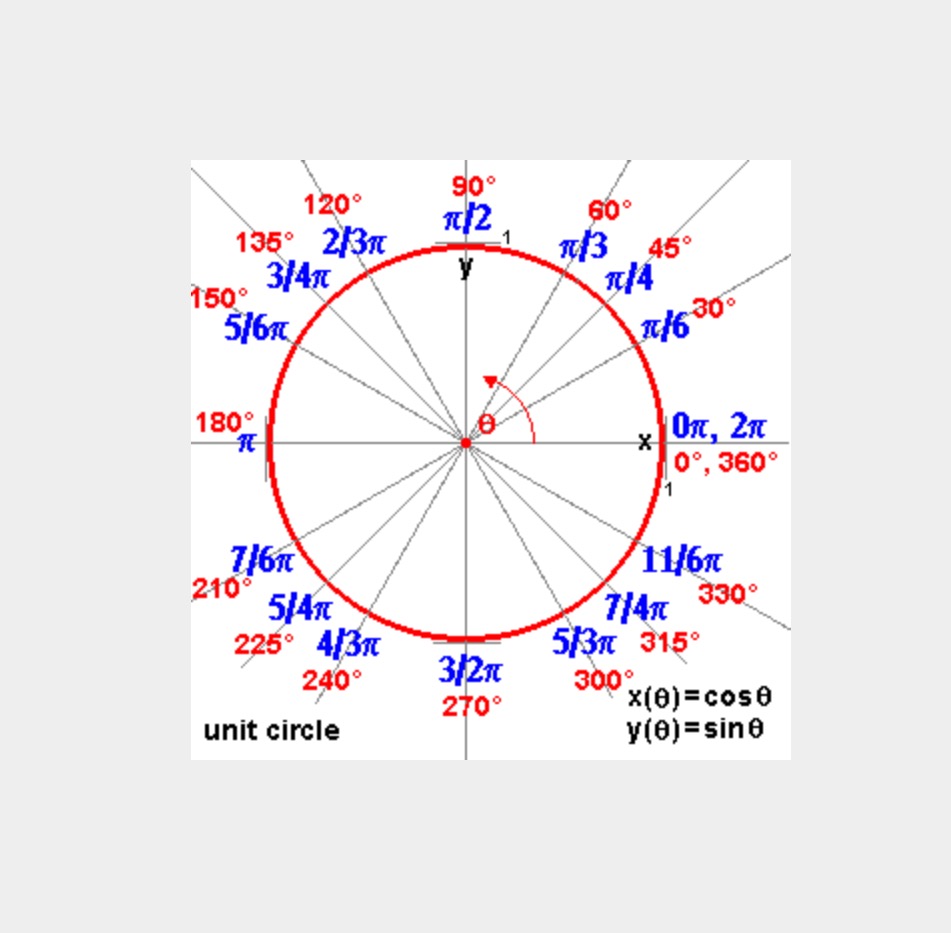
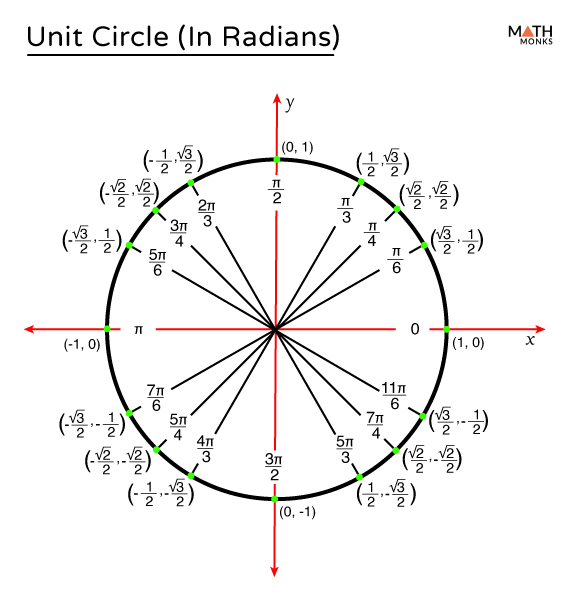
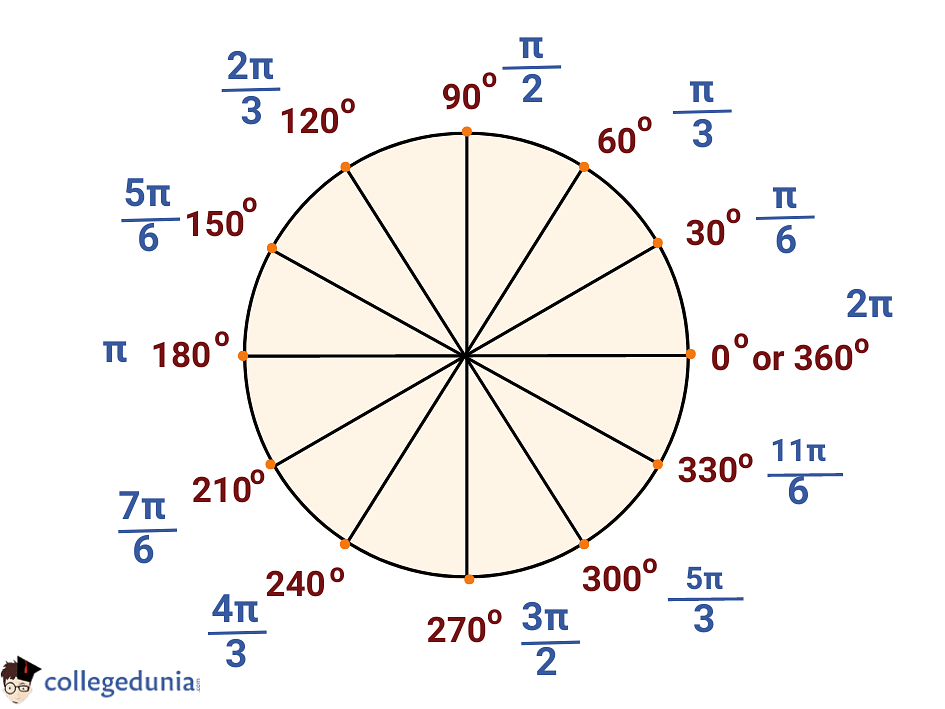
What Is 330 Degrees In Radians - What is 330 degrees in radians? 11π/6 radians, when reduced to lowest fraction in terms of π. Cancel the common factor of 30 30. To convert a measurement in degrees to a measurement in radians, you need to use a conversion formula. To convert degrees to radians, multiply by π 180° π 180 °, since a full circle is 360° 360 ° or 2π 2 π radians. Since pi radians are equal. 11π/6 rad can be expressed as real. 330 degrees is equal to 11π / 6 radians. To convert degrees to radians, multiply by π 180° π 180 °, since a full circle is 360° 360 ° or 2π 2 π radians. Cancel the common factor of 30 30.
To convert degrees to radians, we use the fact that 1 revolution is 360 degrees, which is. Since pi radians are equal. 330 degrees is equal to 11π / 6 radians. 11π/6 radians, when reduced to lowest fraction in terms of π. To convert degrees to radians, multiply by π 180° π 180 °, since a full circle is 360° 360 ° or 2π 2 π radians. Cancel the common factor of 30 30. What is 330 degrees in radians? 330 degrees is equal to 11π/6 radians. To convert degrees to radians, multiply by π 180° π 180 °, since a full circle is 360° 360 ° or 2π 2 π radians. To convert a measurement in degrees to a measurement in radians, you need to use a conversion formula.
330 degrees is equal to 11π/6 radians. Cancel the common factor of 30 30. To convert degrees to radians, we use the fact that 1 revolution is 360 degrees, which is. To convert 330 degrees to radians, we can use the conversion formula: To convert degrees to radians, multiply by π 180° π 180 °, since a full circle is 360° 360 ° or 2π 2 π radians. Cancel the common factor of 30 30. 11π/6 rad can be expressed as real. To convert degrees to radians, multiply by π 180° π 180 °, since a full circle is 360° 360 ° or 2π 2 π radians. To convert a measurement in degrees to a measurement in radians, you need to use a conversion formula. What is 330 degrees in radians?
Unit 7 More Geometry
To convert degrees to radians, we use the fact that 1 revolution is 360 degrees, which is. 11π/6 rad can be expressed as real. To convert a measurement in degrees to a measurement in radians, you need to use a conversion formula. Since pi radians are equal. 330 degrees is equal to 11π/6 radians.
How Many Radians Is Pi
To convert 330 degrees to radians, we can use the conversion formula: 330 degrees is equal to 11π/6 radians. 11π/6 radians, when reduced to lowest fraction in terms of π. To convert degrees to radians, we use the fact that 1 revolution is 360 degrees, which is. To convert a measurement in degrees to a measurement in radians, you need.
Unit Circle Radians Chart
Since pi radians are equal. Cancel the common factor of 30 30. To convert a measurement in degrees to a measurement in radians, you need to use a conversion formula. What is 330 degrees in radians? 330 degrees is equal to 11π/6 radians.
Relation Between Degree and Radian Conversion and Examples
To convert a measurement in degrees to a measurement in radians, you need to use a conversion formula. 11π/6 radians, when reduced to lowest fraction in terms of π. What is 330 degrees in radians? To convert degrees to radians, we use the fact that 1 revolution is 360 degrees, which is. To convert 330 degrees to radians, we can.
FileDegreeRadian Wikipedia, 48 OFF
11π/6 rad can be expressed as real. 330 degrees is equal to 11π / 6 radians. To convert degrees to radians, we use the fact that 1 revolution is 360 degrees, which is. To convert degrees to radians, multiply by π 180° π 180 °, since a full circle is 360° 360 ° or 2π 2 π radians. Since pi.
Radian Conversion Chart
330 degrees is equal to 11π/6 radians. To convert degrees to radians, we use the fact that 1 revolution is 360 degrees, which is. Cancel the common factor of 30 30. 11π/6 radians, when reduced to lowest fraction in terms of π. 11π/6 rad can be expressed as real.
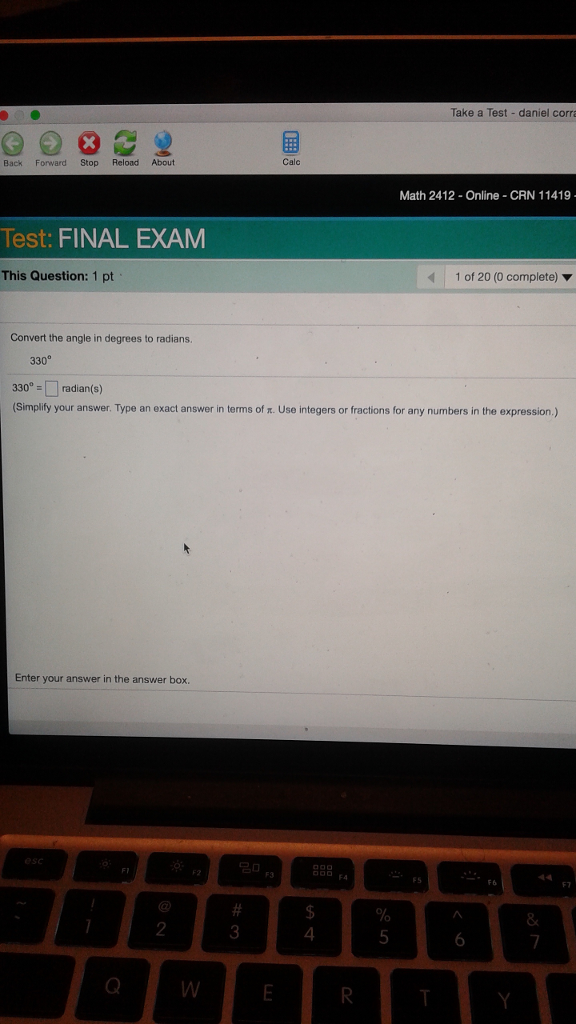
Solved Convert the angle in degrees to radians. 330 degree
Since pi radians are equal. To convert 330 degrees to radians, we can use the conversion formula: To convert degrees to radians, multiply by π 180° π 180 °, since a full circle is 360° 360 ° or 2π 2 π radians. What is 330 degrees in radians? 11π/6 radians, when reduced to lowest fraction in terms of π.
Find the Exact Value of the Tangent of 330 Degrees Using the Unit
To convert degrees to radians, we use the fact that 1 revolution is 360 degrees, which is. 11π/6 radians, when reduced to lowest fraction in terms of π. To convert 330 degrees to radians, we can use the conversion formula: Cancel the common factor of 30 30. 11π/6 rad can be expressed as real.
File30 degree rotations expressed in radian measure.svg Math methods
To convert a measurement in degrees to a measurement in radians, you need to use a conversion formula. Cancel the common factor of 30 30. To convert degrees to radians, multiply by π 180° π 180 °, since a full circle is 360° 360 ° or 2π 2 π radians. To convert degrees to radians, multiply by π 180° π.
Comment convertir des degrés en radians 5 étapes
Cancel the common factor of 30 30. What is 330 degrees in radians? 330 degrees is equal to 11π / 6 radians. To convert a measurement in degrees to a measurement in radians, you need to use a conversion formula. 330 degrees is equal to 11π/6 radians.
11Π/6 Radians, When Reduced To Lowest Fraction In Terms Of Π.
Since pi radians are equal. To convert degrees to radians, multiply by π 180° π 180 °, since a full circle is 360° 360 ° or 2π 2 π radians. 11π/6 rad can be expressed as real. Cancel the common factor of 30 30.
What Is 330 Degrees In Radians?
330 degrees is equal to 11π / 6 radians. To convert 330 degrees to radians, we can use the conversion formula: 330 degrees is equal to 11π/6 radians. To convert degrees to radians, we use the fact that 1 revolution is 360 degrees, which is.
To Convert A Measurement In Degrees To A Measurement In Radians, You Need To Use A Conversion Formula.
Cancel the common factor of 30 30. To convert degrees to radians, multiply by π 180° π 180 °, since a full circle is 360° 360 ° or 2π 2 π radians.