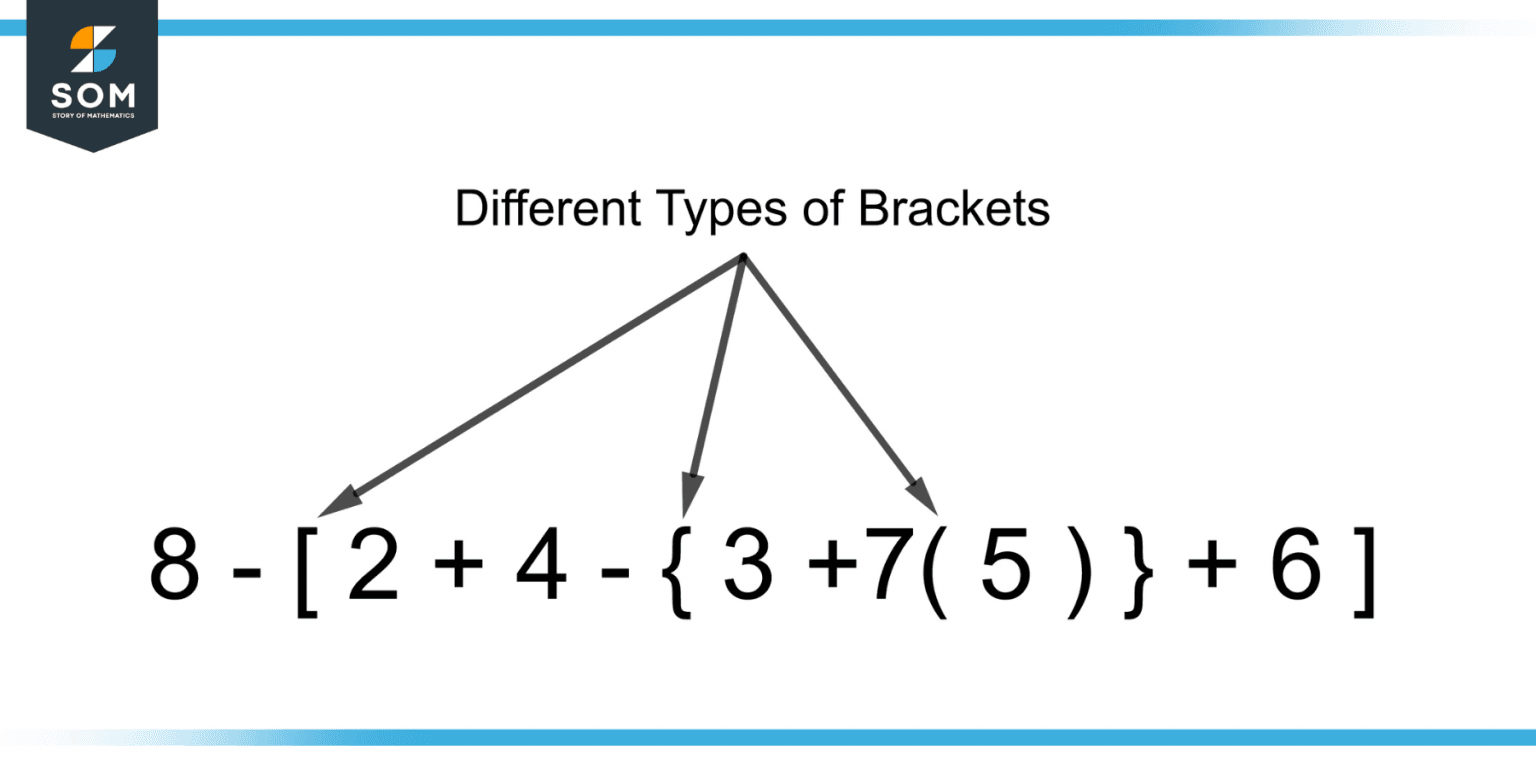
Double Square Brackets Math

Double Square Brackets Math - We can always evaluate the. Indeed, for the usual double square brackets i use \llbracket and \rrbracket, and for the usual large square brackets i use \left[and \right]. With more complicated grouping we can use different types of brackets: Double square brackets $[\![a, b]\!]$ are used also to mean the interval of all integers between a and b included. [(3 + 2) × (6 − 4) + 2] × 4 the parentheses group 3 and 2. The double brackets distinguish it from $\bbb z[t]$, which is the ring of polynomials in $t$ with integer coefficients.

With more complicated grouping we can use different types of brackets: The double brackets distinguish it from $\bbb z[t]$, which is the ring of polynomials in $t$ with integer coefficients. We can always evaluate the. Indeed, for the usual double square brackets i use \llbracket and \rrbracket, and for the usual large square brackets i use \left[and \right]. Double square brackets $[\![a, b]\!]$ are used also to mean the interval of all integers between a and b included. [(3 + 2) × (6 − 4) + 2] × 4 the parentheses group 3 and 2.

The double brackets distinguish it from $\bbb z[t]$, which is the ring of polynomials in $t$ with integer coefficients. [(3 + 2) × (6 − 4) + 2] × 4 the parentheses group 3 and 2. With more complicated grouping we can use different types of brackets: Indeed, for the usual double square brackets i use \llbracket and \rrbracket, and for the usual large square brackets i use \left[and \right]. We can always evaluate the. Double square brackets $[\![a, b]\!]$ are used also to mean the interval of all integers between a and b included.

In math problems, calculate the values within the brackets first Math

Indeed, for the usual double square brackets i use \llbracket and \rrbracket, and for the usual large square brackets i use \left[and \right]. [(3 + 2) × (6 − 4) + 2] × 4 the parentheses group 3 and 2. The double brackets distinguish it from $\bbb z[t]$, which is the ring of polynomials in $t$ with integer coefficients. Double.

symbols LaTeX code for "white square brackets" 〚 and 〛 TeX LaTeX

[(3 + 2) × (6 − 4) + 2] × 4 the parentheses group 3 and 2. Double square brackets $[\![a, b]\!]$ are used also to mean the interval of all integers between a and b included. We can always evaluate the. Indeed, for the usual double square brackets i use \llbracket and \rrbracket, and for the usual large square.

GCSE Maths How to Expand Double Brackets 36 YouTube

We can always evaluate the. With more complicated grouping we can use different types of brackets: Double square brackets $[\![a, b]\!]$ are used also to mean the interval of all integers between a and b included. The double brackets distinguish it from $\bbb z[t]$, which is the ring of polynomials in $t$ with integer coefficients. Indeed, for the usual double.

How To Expand Double Brackets With Powers YouTube

Double square brackets $[\![a, b]\!]$ are used also to mean the interval of all integers between a and b included. [(3 + 2) × (6 − 4) + 2] × 4 the parentheses group 3 and 2. We can always evaluate the. With more complicated grouping we can use different types of brackets: The double brackets distinguish it from $\bbb.

Brackets In Math Definition, Types Examples Video Lesson, 56 OFF

With more complicated grouping we can use different types of brackets: Double square brackets $[\![a, b]\!]$ are used also to mean the interval of all integers between a and b included. The double brackets distinguish it from $\bbb z[t]$, which is the ring of polynomials in $t$ with integer coefficients. [(3 + 2) × (6 − 4) + 2] ×.

How and When To Use Brackets In Grammar [ ] YourDictionary

The double brackets distinguish it from $\bbb z[t]$, which is the ring of polynomials in $t$ with integer coefficients. We can always evaluate the. Indeed, for the usual double square brackets i use \llbracket and \rrbracket, and for the usual large square brackets i use \left[and \right]. With more complicated grouping we can use different types of brackets: Double square.

Expanding double brackets Teaching Resources

We can always evaluate the. [(3 + 2) × (6 − 4) + 2] × 4 the parentheses group 3 and 2. With more complicated grouping we can use different types of brackets: The double brackets distinguish it from $\bbb z[t]$, which is the ring of polynomials in $t$ with integer coefficients. Indeed, for the usual double square brackets i.

Expanding Double Brackets (A) Using the Grid Method Worksheet Cazoom

With more complicated grouping we can use different types of brackets: We can always evaluate the. Double square brackets $[\![a, b]\!]$ are used also to mean the interval of all integers between a and b included. Indeed, for the usual double square brackets i use \llbracket and \rrbracket, and for the usual large square brackets i use \left[and \right]. [(3.

Brackets Definition & Meaning

Double square brackets $[\![a, b]\!]$ are used also to mean the interval of all integers between a and b included. With more complicated grouping we can use different types of brackets: [(3 + 2) × (6 − 4) + 2] × 4 the parentheses group 3 and 2. The double brackets distinguish it from $\bbb z[t]$, which is the ring.

How To Use The 4 Types of Brackets

The double brackets distinguish it from $\bbb z[t]$, which is the ring of polynomials in $t$ with integer coefficients. Double square brackets $[\![a, b]\!]$ are used also to mean the interval of all integers between a and b included. We can always evaluate the. Indeed, for the usual double square brackets i use \llbracket and \rrbracket, and for the usual.

With More Complicated Grouping We Can Use Different Types Of Brackets:

We can always evaluate the. The double brackets distinguish it from $\bbb z[t]$, which is the ring of polynomials in $t$ with integer coefficients. Double square brackets $[\![a, b]\!]$ are used also to mean the interval of all integers between a and b included. [(3 + 2) × (6 − 4) + 2] × 4 the parentheses group 3 and 2.