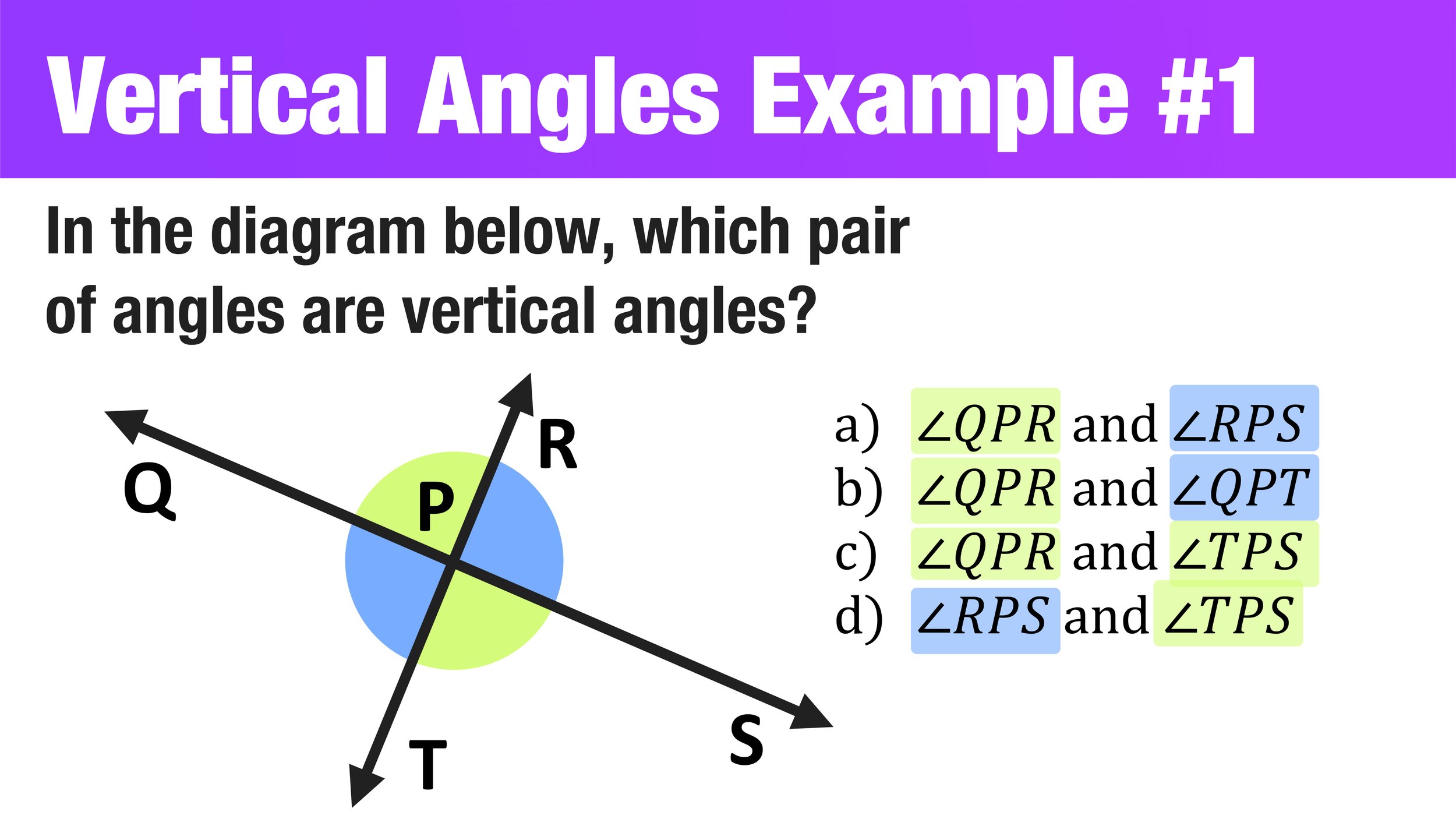
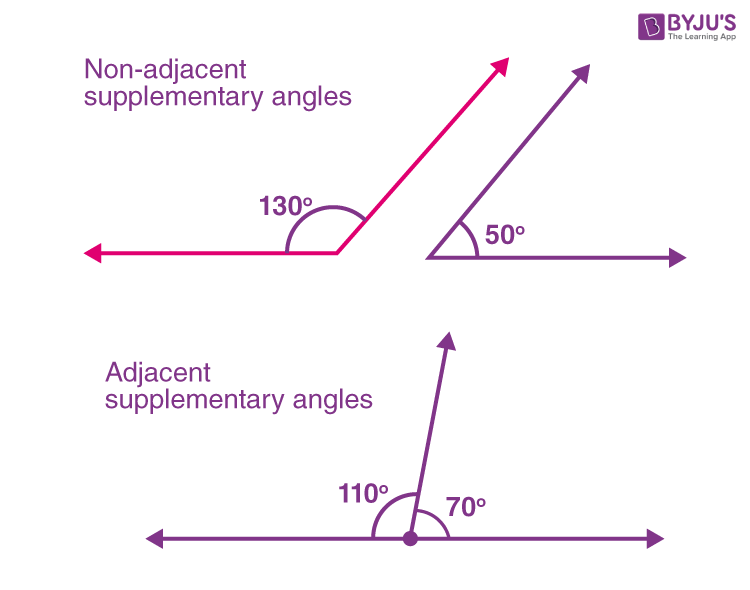
Do Two Vertical Angles Form A Linear Pair - A linear pair is two adjacent. The given statement is false. Let’s quickly go over the definitions what it means to be adjacent. Vertical angles, such as ∠1 and ∠2, form linear pairs with the same angle, ∠4, giving m ∠1 + m∠4 = 180 and m ∠2 + m ∠4 = 180. A linear pair is a pair of two angles that are adjacent and supplementary. When two lines cross, vertical angles are. A linear pair cannot be formed by a pair of vertical angles. Vertical angles are a pair of nonadjacent angles, ∠1 and ∠2, formed by two intersecting lines.
A linear pair cannot be formed by a pair of vertical angles. When two lines cross, vertical angles are. Vertical angles, such as ∠1 and ∠2, form linear pairs with the same angle, ∠4, giving m ∠1 + m∠4 = 180 and m ∠2 + m ∠4 = 180. A linear pair is two adjacent. A linear pair is a pair of two angles that are adjacent and supplementary. Vertical angles are a pair of nonadjacent angles, ∠1 and ∠2, formed by two intersecting lines. Let’s quickly go over the definitions what it means to be adjacent. The given statement is false.
Let’s quickly go over the definitions what it means to be adjacent. A linear pair is a pair of two angles that are adjacent and supplementary. When two lines cross, vertical angles are. Vertical angles, such as ∠1 and ∠2, form linear pairs with the same angle, ∠4, giving m ∠1 + m∠4 = 180 and m ∠2 + m ∠4 = 180. A linear pair cannot be formed by a pair of vertical angles. A linear pair is two adjacent. The given statement is false. Vertical angles are a pair of nonadjacent angles, ∠1 and ∠2, formed by two intersecting lines.
What are Vertical Angles? — Mashup Math
Vertical angles are a pair of nonadjacent angles, ∠1 and ∠2, formed by two intersecting lines. Vertical angles, such as ∠1 and ∠2, form linear pairs with the same angle, ∠4, giving m ∠1 + m∠4 = 180 and m ∠2 + m ∠4 = 180. When two lines cross, vertical angles are. A linear pair is two adjacent. Let’s.
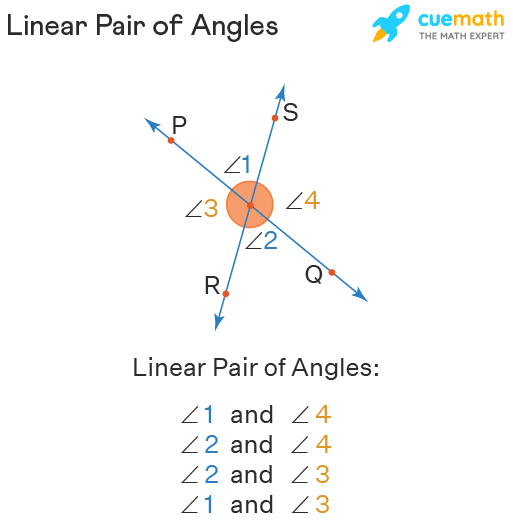
Linear Pair of Angles Definition, Axiom, Examples
A linear pair cannot be formed by a pair of vertical angles. A linear pair is a pair of two angles that are adjacent and supplementary. Let’s quickly go over the definitions what it means to be adjacent. A linear pair is two adjacent. Vertical angles are a pair of nonadjacent angles, ∠1 and ∠2, formed by two intersecting lines.
What Is Vertical Angles Theorem Nelson Bountly
A linear pair is a pair of two angles that are adjacent and supplementary. When two lines cross, vertical angles are. Vertical angles, such as ∠1 and ∠2, form linear pairs with the same angle, ∠4, giving m ∠1 + m∠4 = 180 and m ∠2 + m ∠4 = 180. The given statement is false. Vertical angles are a.
Two angles forming a linear pair are always
Vertical angles, such as ∠1 and ∠2, form linear pairs with the same angle, ∠4, giving m ∠1 + m∠4 = 180 and m ∠2 + m ∠4 = 180. The given statement is false. A linear pair is two adjacent. A linear pair is a pair of two angles that are adjacent and supplementary. Vertical angles are a pair.
Two angles form a linear pair. The measure of one CameraMath
The given statement is false. Let’s quickly go over the definitions what it means to be adjacent. When two lines cross, vertical angles are. A linear pair is a pair of two angles that are adjacent and supplementary. A linear pair is two adjacent.
Which Pair Of Angles Are Vertical Angles
A linear pair is two adjacent. Let’s quickly go over the definitions what it means to be adjacent. A linear pair cannot be formed by a pair of vertical angles. Vertical angles are a pair of nonadjacent angles, ∠1 and ∠2, formed by two intersecting lines. A linear pair is a pair of two angles that are adjacent and supplementary.
Question 1 In the figure (i) Is angle 1 adjacent to 2? (ii) Is AOC
When two lines cross, vertical angles are. Vertical angles are a pair of nonadjacent angles, ∠1 and ∠2, formed by two intersecting lines. Let’s quickly go over the definitions what it means to be adjacent. The given statement is false. A linear pair is a pair of two angles that are adjacent and supplementary.
Day 1 HW Angle Pairs Adjacent, vertical, supplementary, complementary
Vertical angles are a pair of nonadjacent angles, ∠1 and ∠2, formed by two intersecting lines. A linear pair is a pair of two angles that are adjacent and supplementary. A linear pair cannot be formed by a pair of vertical angles. A linear pair is two adjacent. Vertical angles, such as ∠1 and ∠2, form linear pairs with the.
Example of supplementary angle chlistmuscle
When two lines cross, vertical angles are. A linear pair is two adjacent. A linear pair cannot be formed by a pair of vertical angles. Vertical angles are a pair of nonadjacent angles, ∠1 and ∠2, formed by two intersecting lines. Let’s quickly go over the definitions what it means to be adjacent.
What are Vertical Angles? — Mashup Math
Vertical angles are a pair of nonadjacent angles, ∠1 and ∠2, formed by two intersecting lines. The given statement is false. A linear pair cannot be formed by a pair of vertical angles. Vertical angles, such as ∠1 and ∠2, form linear pairs with the same angle, ∠4, giving m ∠1 + m∠4 = 180 and m ∠2 + m.
Vertical Angles Are A Pair Of Nonadjacent Angles, ∠1 And ∠2, Formed By Two Intersecting Lines.
A linear pair cannot be formed by a pair of vertical angles. Let’s quickly go over the definitions what it means to be adjacent. The given statement is false. When two lines cross, vertical angles are.
A Linear Pair Is Two Adjacent.
Vertical angles, such as ∠1 and ∠2, form linear pairs with the same angle, ∠4, giving m ∠1 + m∠4 = 180 and m ∠2 + m ∠4 = 180. A linear pair is a pair of two angles that are adjacent and supplementary.